Problem Sudoku
This well-known problem is stated as follows: fill in a grid using digits ranging from 1 to 9 such that:
- all digits occur on each row
- all digits occur on each column
- all digits occur in each $3 \times 3$ block (starting at a position multiple of 3)
Here is an illustration: 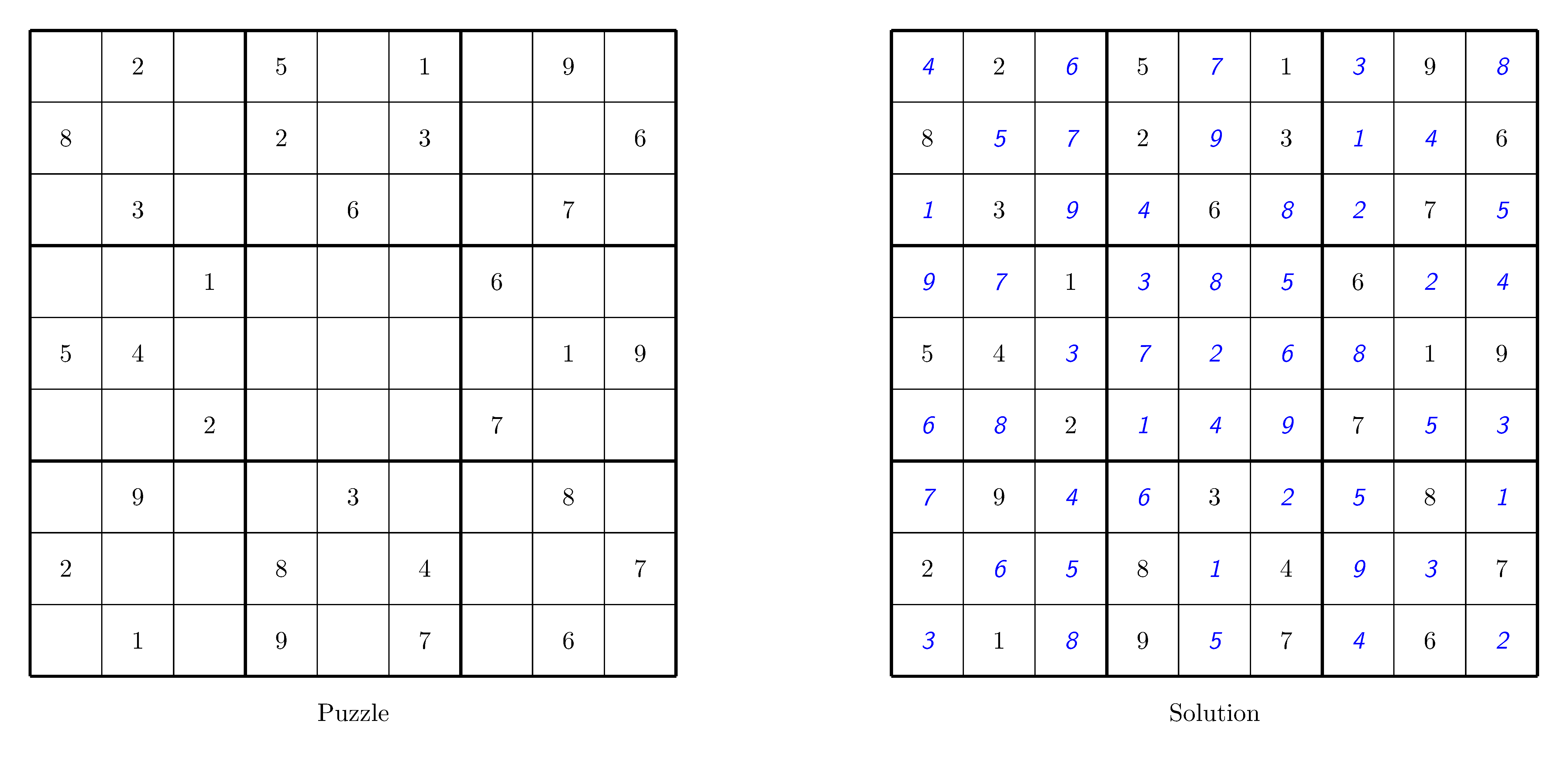
To build a CSP (Constraint Satisfaction Problem) model, we need first to import the library PyCSP$^3$:
from pycsp3 import *
In a first step, we shall build a Sudoku grid from no data/clues (i.e., from an empty grid).
We start our CSP model with a two-dimensional array $x$ of $9 \times 9$ variables, each variable having ${1,2,\dots,9}$ as domain.
# x[i][j] is the value at row i and col j
x = VarArray(size=[9, 9], dom=range(1, 10))
We can display the structure of the array, as well as the domain of the first variable (remember that all variables have the same domain).
print(x)
print("Domain of any variable: ", x[0][0].dom)
[
[x[0][0], x[0][1], x[0][2], x[0][3], x[0][4], x[0][5], x[0][6], x[0][7], x[0][8]]
[x[1][0], x[1][1], x[1][2], x[1][3], x[1][4], x[1][5], x[1][6], x[1][7], x[1][8]]
[x[2][0], x[2][1], x[2][2], x[2][3], x[2][4], x[2][5], x[2][6], x[2][7], x[2][8]]
[x[3][0], x[3][1], x[3][2], x[3][3], x[3][4], x[3][5], x[3][6], x[3][7], x[3][8]]
[x[4][0], x[4][1], x[4][2], x[4][3], x[4][4], x[4][5], x[4][6], x[4][7], x[4][8]]
[x[5][0], x[5][1], x[5][2], x[5][3], x[5][4], x[5][5], x[5][6], x[5][7], x[5][8]]
[x[6][0], x[6][1], x[6][2], x[6][3], x[6][4], x[6][5], x[6][6], x[6][7], x[6][8]]
[x[7][0], x[7][1], x[7][2], x[7][3], x[7][4], x[7][5], x[7][6], x[7][7], x[7][8]]
[x[8][0], x[8][1], x[8][2], x[8][3], x[8][4], x[8][5], x[8][6], x[8][7], x[8][8]]
]
Domain of any variable: 1..9
Interestingly, with a single constraint AllDifferentMatrix, we can impose that all digits are different on each row and column of $x$.
satisfy(
# imposing distinct values on each row and each column
AllDifferent(x, matrix=True)
);
By calling the function solve(), we can check that the problem is satisfiable (SAT). We can also display the found solution. Here, we call the function values() that collects the values assigned to a specified list of variables.
if solve() is SAT:
for i in range(9):
print(values(x[i]))
[1, 2, 3, 4, 5, 6, 7, 8, 9]
[2, 1, 4, 3, 6, 5, 8, 9, 7]
[3, 4, 1, 2, 7, 8, 9, 5, 6]
[4, 3, 2, 1, 8, 9, 6, 7, 5]
[5, 6, 7, 8, 9, 1, 2, 3, 4]
[6, 5, 8, 9, 1, 7, 3, 4, 2]
[7, 8, 9, 5, 2, 3, 4, 6, 1]
[8, 9, 6, 7, 4, 2, 5, 1, 3]
[9, 7, 5, 6, 3, 4, 1, 2, 8]
Note that we get a structured string representation of multi-dimensional lists when printing them directly.
if solve() is SAT:
print(values(x))
[
[1, 2, 3, 4, 5, 6, 7, 8, 9]
[2, 1, 4, 3, 6, 5, 8, 9, 7]
[3, 4, 1, 2, 7, 8, 9, 5, 6]
[4, 3, 2, 1, 8, 9, 6, 7, 5]
[5, 6, 7, 8, 9, 1, 2, 3, 4]
[6, 5, 8, 9, 1, 7, 3, 4, 2]
[7, 8, 9, 5, 2, 3, 4, 6, 1]
[8, 9, 6, 7, 4, 2, 5, 1, 3]
[9, 7, 5, 6, 3, 4, 1, 2, 8]
]
On can observe that some digits occur several times in the same block. This is why we add a list of constraints AllDifferent.
satisfy(
# imposing distinct values on each block
AllDifferent(x[i:i + 3, j:j + 3]) for i in [0, 3, 6] for j in [0, 3, 6]
);
Note how the notation $x[i:i + 3, j:j + 3]$ extracts a list of variables corresponding to a block of size $3 \times 3$ in $x$. This is similar to notations used in package NumPy. We can check this:
print(x[0:3,0:3])
[
[x[0][0], x[0][1], x[0][2]]
[x[1][0], x[1][1], x[1][2]]
[x[2][0], x[2][1], x[2][2]]
]
We can control the scope (i.e., involved variables) of all posted constraints by displaying their internal representation.
print(posted())
allDifferent(matrix:x[][])
allDifferent(list:[x[0][0], x[0][1], x[0][2], x[1][0], x[1][1], x[1][2], x[2][0], x[2][1], x[2][2]])
allDifferent(list:[x[0][3], x[0][4], x[0][5], x[1][3], x[1][4], x[1][5], x[2][3], x[2][4], x[2][5]])
allDifferent(list:[x[0][6], x[0][7], x[0][8], x[1][6], x[1][7], x[1][8], x[2][6], x[2][7], x[2][8]])
allDifferent(list:[x[3][0], x[3][1], x[3][2], x[4][0], x[4][1], x[4][2], x[5][0], x[5][1], x[5][2]])
allDifferent(list:[x[3][3], x[3][4], x[3][5], x[4][3], x[4][4], x[4][5], x[5][3], x[5][4], x[5][5]])
allDifferent(list:[x[3][6], x[3][7], x[3][8], x[4][6], x[4][7], x[4][8], x[5][6], x[5][7], x[5][8]])
allDifferent(list:[x[6][0], x[6][1], x[6][2], x[7][0], x[7][1], x[7][2], x[8][0], x[8][1], x[8][2]])
allDifferent(list:[x[6][3], x[6][4], x[6][5], x[7][3], x[7][4], x[7][5], x[8][3], x[8][4], x[8][5]])
allDifferent(list:[x[6][6], x[6][7], x[6][8], x[7][6], x[7][7], x[7][8], x[8][6], x[8][7], x[8][8]])
Now, we can generate a valid Sudoku grid.
if solve() is SAT:
print(values(x))
[
[1, 2, 3, 4, 5, 6, 7, 8, 9]
[4, 5, 6, 7, 8, 9, 1, 2, 3]
[7, 8, 9, 1, 2, 3, 4, 5, 6]
[2, 1, 4, 3, 6, 5, 8, 9, 7]
[3, 6, 5, 8, 9, 7, 2, 1, 4]
[8, 9, 7, 2, 1, 4, 3, 6, 5]
[5, 3, 1, 6, 4, 2, 9, 7, 8]
[6, 4, 2, 9, 7, 8, 5, 3, 1]
[9, 7, 8, 5, 3, 1, 6, 4, 2]
]
In a second step, we decide to take into account the clues as those in the illustration above. When 0 is present in a cell, it means that no clue is given for this cell.
clues = [
[0, 2, 0, 5, 0, 1, 0, 9, 0],
[8, 0, 0, 2, 0, 3, 0, 0, 6],
[0, 3, 0, 0, 6, 0, 0, 7, 0],
[0, 0, 1, 0, 0, 0, 6, 0, 0],
[5, 4, 0, 0, 0, 0, 0, 1, 9],
[0, 0, 2, 0, 0, 0, 7, 0, 0],
[0, 9, 0, 0, 3, 0, 0, 8, 0],
[2, 0, 0, 8, 0, 4, 0, 0, 7],
[0, 1, 0, 9, 0, 7, 0, 6, 0]
]
We can post an unary constraint Intension for any given clue.
satisfy (
# imposing clues
x[i][j] == clues[i][j] for i in range(9) for j in range(9) if clues[i][j] > 0
);
We can control that such instantiations are well defined by displaying, for example, the internal representation of the last posted constraint.
print(posted(-1,-1))
intension(function:eq(x[8][7],6))
We can now find a solution for that grid.
if solve() is SAT:
print(values(x))
[
[4, 2, 6, 5, 7, 1, 3, 9, 8]
[8, 5, 7, 2, 9, 3, 1, 4, 6]
[1, 3, 9, 4, 6, 8, 2, 7, 5]
[9, 7, 1, 3, 8, 5, 6, 2, 4]
[5, 4, 3, 7, 2, 6, 8, 1, 9]
[6, 8, 2, 1, 4, 9, 7, 5, 3]
[7, 9, 4, 6, 3, 2, 5, 8, 1]
[2, 6, 5, 8, 1, 4, 9, 3, 7]
[3, 1, 8, 9, 5, 7, 4, 6, 2]
]
Most of the time, there is only one solution for a Sudoku puzzle. We can check this here:
if solve(sols=ALL) is SAT:
print("Number of solutions: ", n_solutions())
Number of solutions: 1
Finally, we give below the model in one piece. Here the data is expected to be given by the user (in a command line).
from pycsp3 import *
clues = data # if not 0, clues[i][j] is a value imposed at row i and col j
# x[i][j] is the value at row i and col j
x = VarArray(size=[9, 9], dom=range(1, 10))
satisfy(
# imposing distinct values on each row and each column
AllDifferent(x, matrix=True),
# imposing distinct values on each block tag(blocks)
[AllDifferent(x[i:i + 3, j:j + 3]) for i in [0, 3, 6] for j in [0, 3, 6]],
# imposing clues tag(clues)
[x[i][j] == clues[i][j] for i in range(9) for j in range(9) if clues and clues[i][j] > 0]
)