CSP medium

Problem Nonogram

From CSPLib: Nonograms are a popular puzzle, which goes by different names in different countries. Solvers have to shade in squares in a grid so that blocks of consecutive shaded squares satisfy constraints given for each row and column. Constraints typically indicate the sequence of shaded blocks (e.g. 3,1,2 means that there is a block of 3, then a gap of unspecified size, a block of length 1, another gap, and then a block of length 2). Below, there is an example (taken from Chapter 14 in Gecode documentation):

Puzzle: Nonogram Puzzle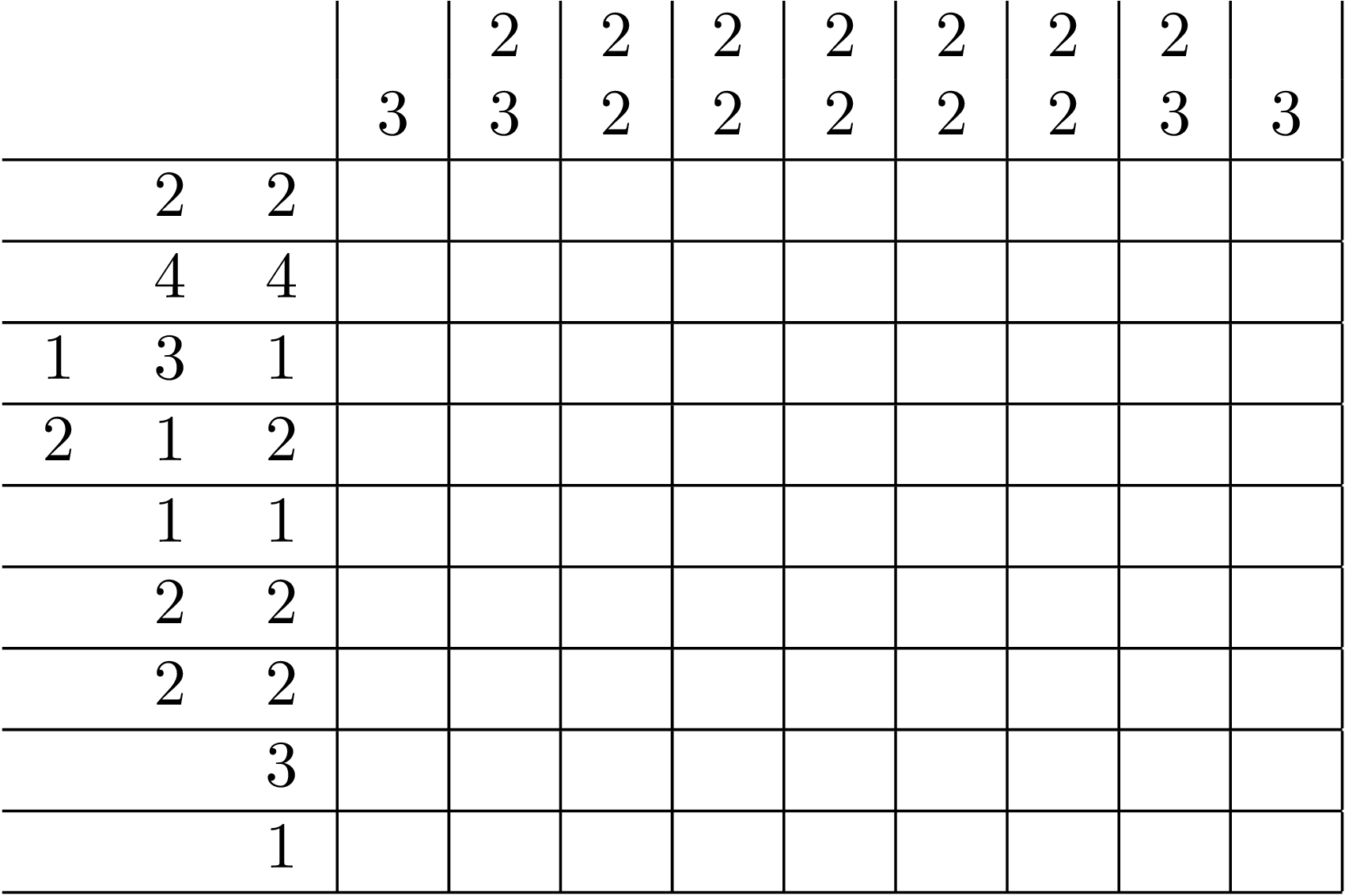

Solution: 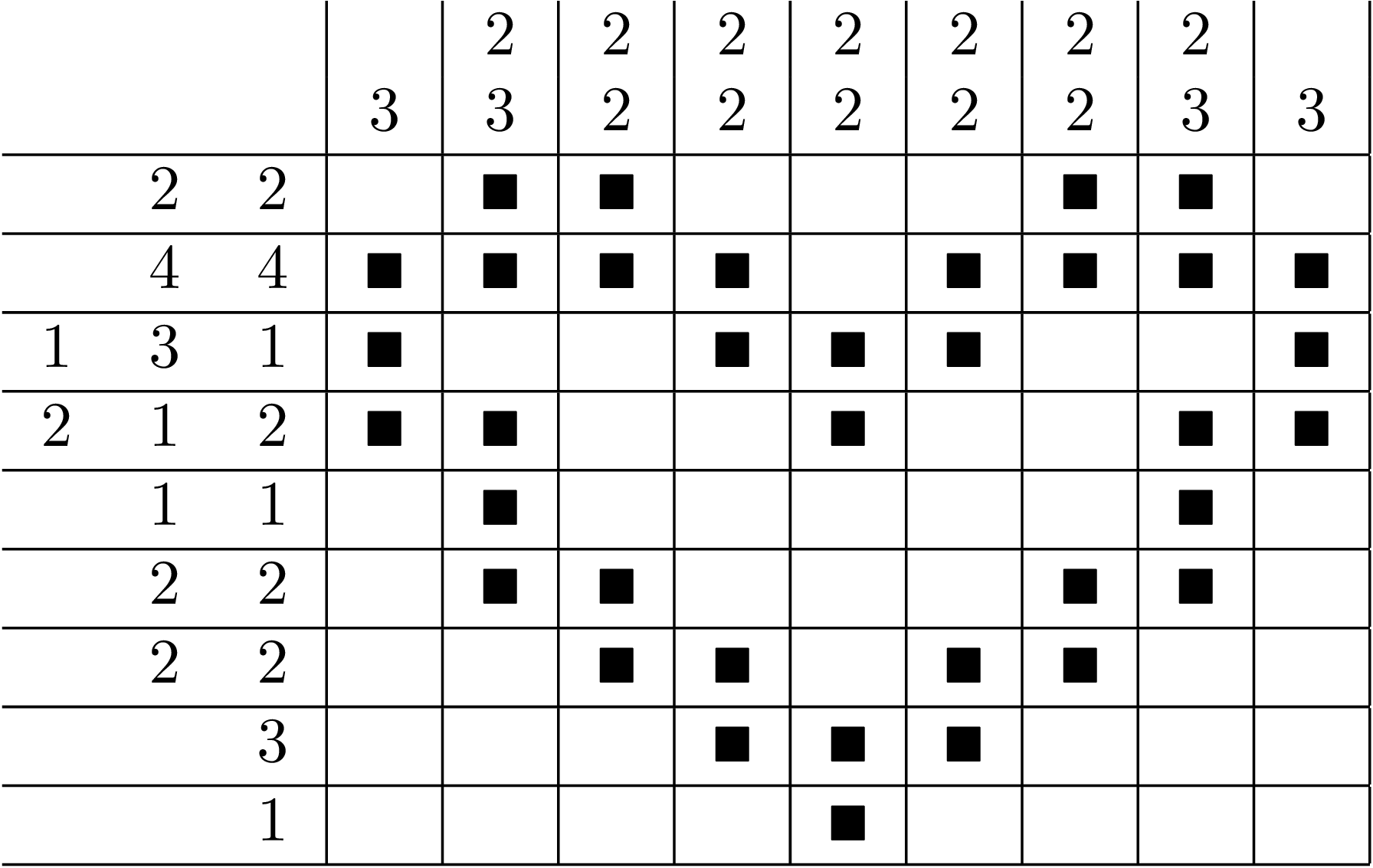Nonogram Solution

To build a CSP (Constraint Satisfaction Problem) model, we need first to import the library PyCSP$^3$:

from pycsp3 import *

Suppose that the data (for a specific Nonogram puzzle) are initially given in a text file as follows:

a line stating the numbers of rows and columns,
then, for each row a line stating the number of blocks followed by the sizes of all these blocks (on the same line),
then, for each column a line stating the number of blocks followed by the sizes of all these blocks (on the same line).

It is possible to loas such a file, for example with:

from pycsp3.problems.data.parsing import register_fields, next_int

register_fields("https://www.cril.univ-artois.fr/~lecoutre/heart.txt")

nRows, nCols = next_int(), next_int()
rows = [[next_int() for _ in range(next_int())] for _ in range(nRows)]
cols = [[next_int() for _ in range(next_int())] for _ in range(nRows)]

However, here, we will consider a JSON file. Actually, this file can be found here. To load block patterns, we can then execute:

rows, cols = default_data("https://www.cril.univ-artois.fr/~lecoutre/heart.json")
nRows, nCols = len(rows), len(cols)

---------------------------------------------------------------------------

ConnectionResetError                      Traceback (most recent call last)

File /usr/lib/python3.10/urllib/request.py:1348, in AbstractHTTPHandler.do_open(self, http_class, req, **http_conn_args)
   1347 try:
-> 1348     h.request(req.get_method(), req.selector, req.data, headers,
   1349               encode_chunked=req.has_header('Transfer-encoding'))
   1350 except OSError as err: # timeout error


File /usr/lib/python3.10/http/client.py:1283, in HTTPConnection.request(self, method, url, body, headers, encode_chunked)
   1282 """Send a complete request to the server."""
-> 1283 self._send_request(method, url, body, headers, encode_chunked)


File /usr/lib/python3.10/http/client.py:1329, in HTTPConnection._send_request(self, method, url, body, headers, encode_chunked)
   1328     body = _encode(body, 'body')
-> 1329 self.endheaders(body, encode_chunked=encode_chunked)


File /usr/lib/python3.10/http/client.py:1278, in HTTPConnection.endheaders(self, message_body, encode_chunked)
   1277     raise CannotSendHeader()
-> 1278 self._send_output(message_body, encode_chunked=encode_chunked)


File /usr/lib/python3.10/http/client.py:1038, in HTTPConnection._send_output(self, message_body, encode_chunked)
   1037 del self._buffer[:]
-> 1038 self.send(msg)
   1040 if message_body is not None:
   1041 
   1042     # create a consistent interface to message_body


File /usr/lib/python3.10/http/client.py:976, in HTTPConnection.send(self, data)
    975 if self.auto_open:
--> 976     self.connect()
    977 else:


File /usr/lib/python3.10/http/client.py:1455, in HTTPSConnection.connect(self)
   1453     server_hostname = self.host
-> 1455 self.sock = self._context.wrap_socket(self.sock,
   1456                                       server_hostname=server_hostname)


File /usr/lib/python3.10/ssl.py:513, in SSLContext.wrap_socket(self, sock, server_side, do_handshake_on_connect, suppress_ragged_eofs, server_hostname, session)
    507 def wrap_socket(self, sock, server_side=False,
    508                 do_handshake_on_connect=True,
    509                 suppress_ragged_eofs=True,
    510                 server_hostname=None, session=None):
    511     # SSLSocket class handles server_hostname encoding before it calls
    512     # ctx._wrap_socket()
--> 513     return self.sslsocket_class._create(
    514         sock=sock,
    515         server_side=server_side,
    516         do_handshake_on_connect=do_handshake_on_connect,
    517         suppress_ragged_eofs=suppress_ragged_eofs,
    518         server_hostname=server_hostname,
    519         context=self,
    520         session=session
    521     )


File /usr/lib/python3.10/ssl.py:1071, in SSLSocket._create(cls, sock, server_side, do_handshake_on_connect, suppress_ragged_eofs, server_hostname, context, session)
   1070             raise ValueError("do_handshake_on_connect should not be specified for non-blocking sockets")
-> 1071         self.do_handshake()
   1072 except (OSError, ValueError):


File /usr/lib/python3.10/ssl.py:1342, in SSLSocket.do_handshake(self, block)
   1341         self.settimeout(None)
-> 1342     self._sslobj.do_handshake()
   1343 finally:


ConnectionResetError: [Errno 104] Connection reset by peer


During handling of the above exception, another exception occurred:


URLError                                  Traceback (most recent call last)

Cell In[2], line 1
----> 1 rows, cols = default_data("https://www.cril.univ-artois.fr/~lecoutre/heart.json")
      2 nRows, nCols = len(rows), len(cols)


File ~/workspacePy/pycsp3/compiler.py:251, in default_data(filename)
    244 def default_data(filename):
    245     """
    246     Loads data from the specified JSON file (possibly given by an URL)
    247 
    248     :param filename: mane (possibly ULR) of a JSON file
    249     :return: the loaded data
    250     """
--> 251     return load_json_data(filename, storing=True)


File ~/workspacePy/pycsp3/compiler.py:222, in load_json_data(filename, storing)
    220 if filename.startswith("http"):
    221     from urllib.request import urlopen
--> 222     data = json.loads(urlopen(filename).read(), object_pairs_hook=OrderedDict)
    223 else:
    224     if os.path.exists(filename):


File /usr/lib/python3.10/urllib/request.py:216, in urlopen(url, data, timeout, cafile, capath, cadefault, context)
    214 else:
    215     opener = _opener
--> 216 return opener.open(url, data, timeout)


File /usr/lib/python3.10/urllib/request.py:519, in OpenerDirector.open(self, fullurl, data, timeout)
    516     req = meth(req)
    518 sys.audit('urllib.Request', req.full_url, req.data, req.headers, req.get_method())
--> 519 response = self._open(req, data)
    521 # post-process response
    522 meth_name = protocol+"_response"


File /usr/lib/python3.10/urllib/request.py:536, in OpenerDirector._open(self, req, data)
    533     return result
    535 protocol = req.type
--> 536 result = self._call_chain(self.handle_open, protocol, protocol +
    537                           '_open', req)
    538 if result:
    539     return result


File /usr/lib/python3.10/urllib/request.py:496, in OpenerDirector._call_chain(self, chain, kind, meth_name, *args)
    494 for handler in handlers:
    495     func = getattr(handler, meth_name)
--> 496     result = func(*args)
    497     if result is not None:
    498         return result


File /usr/lib/python3.10/urllib/request.py:1391, in HTTPSHandler.https_open(self, req)
   1390 def https_open(self, req):
-> 1391     return self.do_open(http.client.HTTPSConnection, req,
   1392         context=self._context, check_hostname=self._check_hostname)


File /usr/lib/python3.10/urllib/request.py:1351, in AbstractHTTPHandler.do_open(self, http_class, req, **http_conn_args)
   1348         h.request(req.get_method(), req.selector, req.data, headers,
   1349                   encode_chunked=req.has_header('Transfer-encoding'))
   1350     except OSError as err: # timeout error
-> 1351         raise URLError(err)
   1352     r = h.getresponse()
   1353 except:


URLError: <urlopen error [Errno 104] Connection reset by peer>

We can check data:

print("Patterns for rows: ", rows)
print("Patterns for columns: ", cols)

We start our CSP model with a two-dimensional array $x$ of variables, each variable having {0,1} as domain.

# x[i][j] is 1 iff the cell at row i and col j is colored in black
x = VarArray(size=[nRows, nCols], dom={0, 1})

We can display (the structure of) the array as well as the domain of the first variable.

print("Array of variables x: ", x)
print("Domain of any variable: ", x[0][0].dom)

We need to post a constraint Regular per row and per column. Indeed, one can transform any clue (pattern for a row or column) into an automaton. We use this function:

def automaton(pattern):
    q = Automaton.q  # for building state names
    transitions = []
    if len(pattern) == 0:
        n_states = 1
        transitions.append((q(0), 0, q(0)))
    else:
        n_states = sum(pattern) + len(pattern)
        num = 0
        for i, size in enumerate(pattern):
            transitions.append((q(num), 0, q(num)))
            transitions.extend((q(num + j), 1, q(num + j + 1)) for j in range(size))
            transitions.append((q(num + size), 0, q(num + size + (1 if i < len(pattern) - 1 else 0))))
            num += size + 1
    return Automaton(start=q(0), final=q(n_states - 1), transitions=transitions)

For example, if we display the automaton corresponding to the clue (2 2) given for the first row, we can check that the automaton is well built.

print(automaton(rows[0]))

We can now post the constraints Regular:

satisfy(
    [x[i] in automaton(rows[i]) for i in range(nRows)],

    [x[:,j] in automaton(cols[j]) for j in range(nCols)]
);

Interestingly, by calling the function solve(), we can check that the problem is satisfiable (SAT). We can also display the found solution. Here, we call the function values() that collects the values assigned to a specified list of variables.

if solve() is SAT:
    print(values(x))

We can improve the output:

if solve() is SAT:
    for i in range(nRows):
        print(' '.join('*' if value(x[i][j]) == 1 else ' ' for j in range(nCols)))

Finally, we give below the model in one piece. Here the data is expected to be given by the user (in a command line).

from pycsp3 import *

rows, cols = data  # patterns for row and columns
nRows, nCols = len(rows), len(cols)

# x[i][j] is 1 iff the cell at row i and col j is colored in black
x = VarArray(size=[nRows, nCols], dom={0, 1})


def automaton(pattern):
    q = Automaton.q  # for building state names
    transitions = []
    if len(pattern) == 0:
        n_states = 1
        transitions.append((q(0), 0, q(0)))
    else:
        n_states = sum(pattern) + len(pattern)
        num = 0
        for i, size in enumerate(pattern):
            transitions.append((q(num), 0, q(num)))
            transitions.extend((q(num + j), 1, q(num + j + 1)) for j in range(size))
            transitions.append((q(num + size), 0, q(num + size + (1 if i < len(pattern) - 1 else 0))))
            num += size + 1
    return Automaton(start=q(0), final=q(n_states - 1), transitions=transitions)


satisfy(
    [x[i] in automaton(rows[i]) for i in range(nRows)],

    [x[:, j] in automaton(cols[j]) for j in range(nCols)]
)