PyCSP3
PyCSP3 is a Python library for developping models of combinatorial constrained problems in a declarative manner; you can write models of constraint satisfaction (CSP) and constraint optimization (COP) problems. In this website, you will find all that you need to know about Constraint Programming (CP) and PyCSP3, with more than 60 Jupyter Notebooks:
- find the 25 popular constraints , with dedicated Jupyter Notebooks
- discover, step by step, more than 30 models of classical problems (Sport Scheduling, Social Golfers, Warehouse Location , ...), with dedicated Jupyter Notebooks
You can also:
- read this well-documented guide
- explore a GitHub repository containing more than 340 models at pycsp3-models
As an illustration, below, you can find different examples of PyCSP3 models:
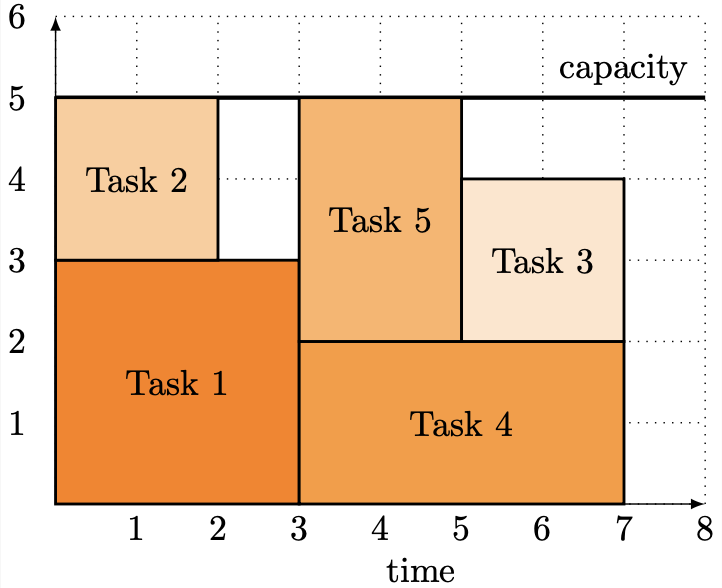
Resource-Constrained Project Scheduling
Finding a non-preemptive schedule of minimal duration by assigning a start time to each activity such that precedence relations and resource availabilities are respected.
durations, successors, quantities, horizon, capacities = data
nJobs = len(durations)
# s[i] is the starting time of the ith job
s = VarArray(size=nJobs, dom=range(horizon))
satisfy(
# job precedence constraints
[
s[i] + durations[i] <= s[j]
for i in range(nJobs) for j in successors[i]]
],
# cumulative resource constraints
[
Cumulative(
Task(
origin=s[i],
length=durations[i],
height=quantities[i][k]
) for i in range(nJobs)
) <= capacity for k, capacity in enumerate(capacities)
]
)
minimize(s[-1])
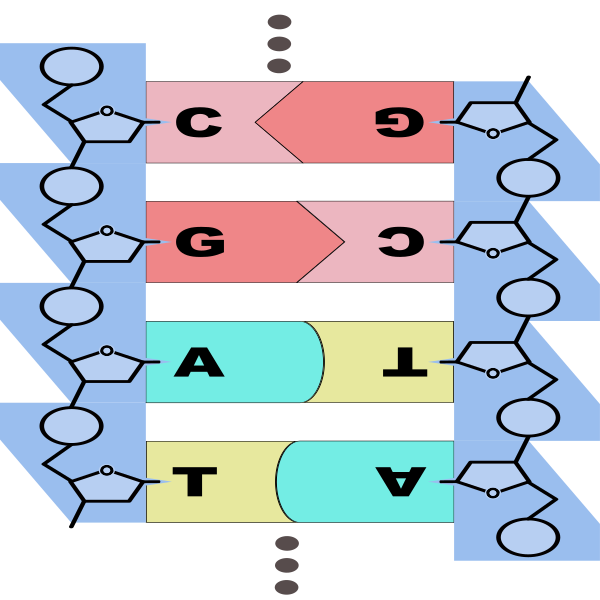
Word Design for DNA
Finding as large as possible a set of strings (words) of length 8 over the alphabet W = {A, C, G, T } with some properties.
words, transitions, n = data
M = MDD(transitions)
# x[i][k] is the kth letter (0-A, 1-C, 2-G, 3-T) of the ith word
x = VarArray(size=[n, 8], dom=range(4))
satisfy(
# each word must be well-formed
[x[i] in words for i in range(n)],
# ordering words tag(symmetry-breaking)
LexIncreasing(x, strict=True),
# ensuring the validity of any pair of words
[x[i] + x[j] in M for i, j in combinations(n, 2)]
)
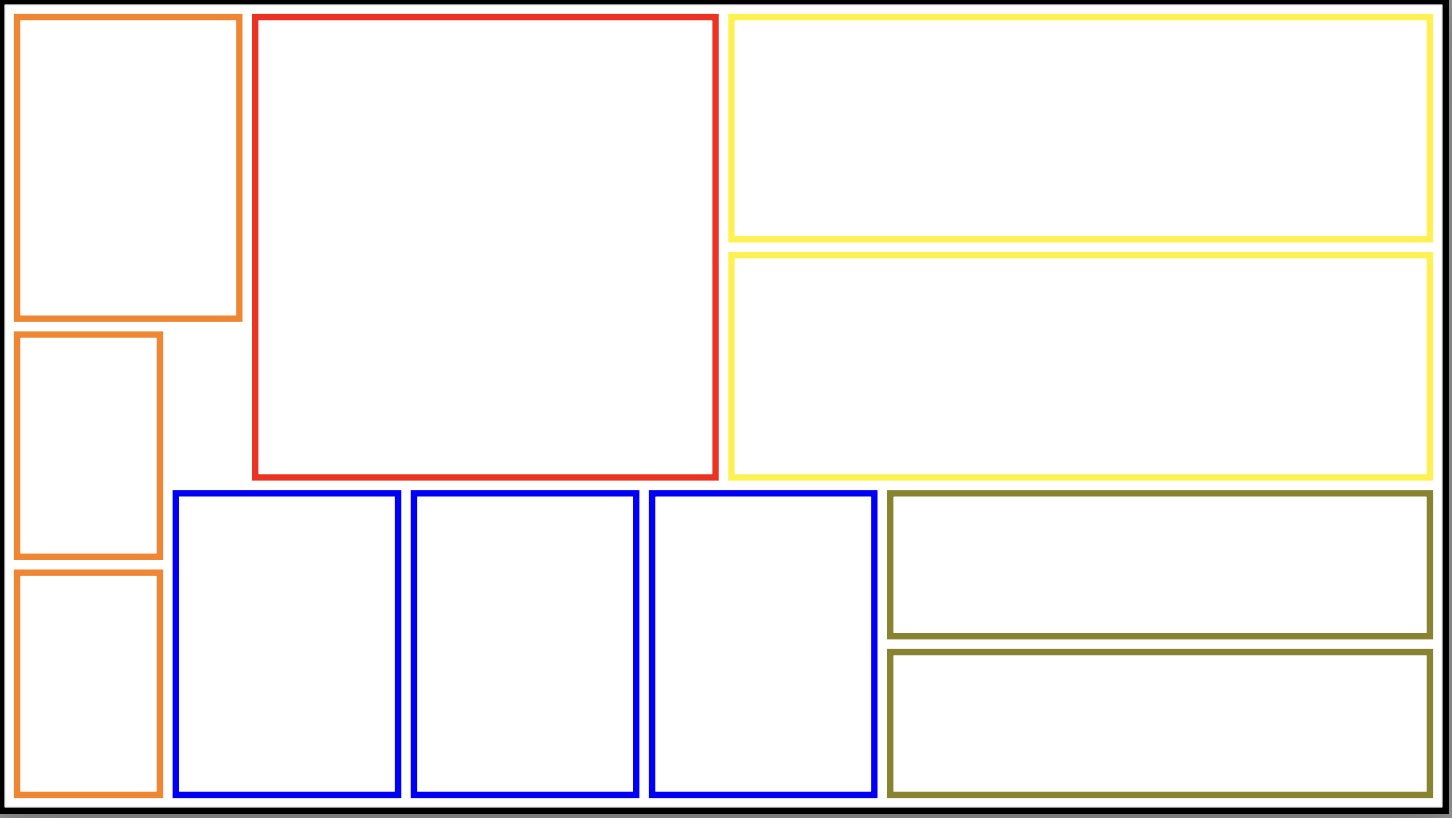
Rectangle Packing
Finding a way of putting a given set of rectangles (boxes) in an enclosing rectangle (container) without overlap.
width, height, boxes = data
nBoxes = len(boxes)
# x[i] is the x-coordinate where is put the ith box (rectangle)
x = VarArray(size=nBoxes, dom=range(width))
# y[i] is the y-coordinate where is put the ith box (rectangle)
y = VarArray(size=nBoxes, dom=range(height))
satisfy(
# unary constraints on x
[x[i] + boxes[i].width <= width for i in range(nBoxes)],
# unary constraints on y
[y[i] + boxes[i].height <= height for i in range(nBoxes)],
# no overlap on boxes
NoOverlap(
origins=[(x[i], y[i]) for i in range(nBoxes)],
lengths=boxes
)
)
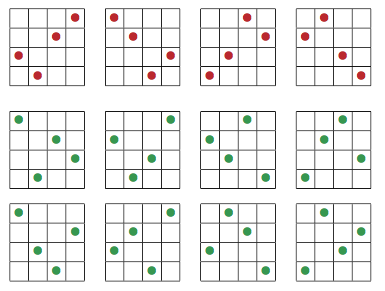
Hamming vectors
Building n vectors of length m with d possible values, while ensuring that the Hamming distance (i.e., the number of distinct elements) is at least equal to k.
n, m, d, k = data or (9, 4, 3, 3)
# x[i][j] is the jth value of the ith vector
x = VarArray(size=[n, m], dom=range(d))
satisfy(
# ensuring a Hamming distance of at least 'k' between any two vectors
[Hamming(row1, row2) >= k for row1, row2 in combinations(x, 2)],
# tag(symmetry-breaking)
LexIncreasing(x)
)

Social Golfers
Scheduling G groups of K golfers over at most W weeks, such that no golfer plays in the same group as any other golfer twice.
nGroups, size, nWeeks, nPlayers = data
# g[w][p] is the group admitting on week w the player p
g = VarArray(size=[nWeeks, nPlayers], dom=range(nGroups))
satisfy(
# ensuring that two players don't meet more than one time
[
If(
g[w1][p1] == g[w1][p2],
Then=g[w2][p1] != g[w2][p2]
) for w1, w2 in combinations(nWeeks, 2)
for p1, p2 in combinations(nPlayers, 2)
],
# respecting the size of the groups
[
Cardinality(
g[w],
occurrences={i: size for i in range(nGroups)}
) for w in range(nWeeks)
]
)

Costas Arrays
Finding a pattern of n marks on an n × n grid, one mark per row and one per column, in which the displacement vectors between the marks are all-different.
n = data
# x[i] is the row where is put the ith mark (on the ith column)
x = VarArray(size=n, dom=range(n))
satisfy(
# all marks are on different rows (and columns)
AllDifferent(x),
# all displacement vectors between the marks must be different
[
AllDifferent(x[i] - x[i + d] for i in range(n - d)) for d in range(1, n - 1)
]
)
Last News
- December 10, 2023
- New GitHub repository for Models and Data; see pycsp3-models and this page.
- December 10, 2023
- PyCSP3 2.2, with new (control) structures 'If' and 'Match', new derivated constraint forms (Hamming, Exist, NotExist, ExactlyOne, AtLeastOne, AtMostOne and AllHold), new functions 'both' and 'either', auto-adjustment of array indexing, and the predefined named tuple 'Task'. See other extensions in Changelog Chapter of the complete guide.
- August 30, 2023
- 2023 XCSP3 Competition, held with CP 2023; see the results.
- November 10, 2022
- PyCSP3 2.1, with new versions of embedded solvers (ACE and Choco) and additional constraints (Precedence, BinPacking, Knapsack, MinimumArg, MaximumArg).
- November 10, 2022
- Specifications of XCSP3, Version 3.1
- November 10, 2022
- ACE 2.1 , Version 2.1 of the generic constraint solver ACE (written in Java).
- August 3, 2022
- 2022 XCSP3 Competition, held with FLoC 2022 (Olympic Games); see the results.
- December 15, 2021
- PyCSP3 2.0 , Version 2 of the Python library PyCSP3.
- December 15, 2021
- ACE 2.0 , Version 2 of the generic constraint solver ACE (written in Java).
- January 16, 2021
- Specifications of XCSP3, Version 3.0.7
Requirements
- For building and compiling models, you need:
- Python 3.10 (at least) to be installed.
- Python package PyCSP3 to be installed, for example from PyPi:
pip install pycsp3
- For running the embedded solvers (ACE and Choco), you need Java 11 to be installed
Importantly, there is a complete separation between the modeling and solving phases: you write a model, you compile it (while providing some data) in order to generate an XCSP3 instance (file), and you solve that problem instance by means of a constraint solver. You can also directly pilot the solving procedure in PyCSP3 possibly conducting an incremental solving strategy.
In a nutshell, the main ingredients of the complete tool chain we propose for handling combinatorial constrained problems are:
- PyCSP3: a Python library for modelling constrained problems, which is described in this document
- XCSP3: an intermediate format used to represent problem instances while preserving structure of models
A shown in the figure below, the user who wishes to solve a combinatorial constrained problem has to:
- write a model using the Python library PyCSP3 (i.e., write a Python file)
- provide a data file (in JSON format) for a specific problem instance to be solved
- compile both files (model and data) so as to generate an XCSP3 instance (file)
- solve the XCSP3 file (problem instance under format XCSP3) by using a constraint solver as, e.g., ACE, Choco, OscaR or PicatSAT
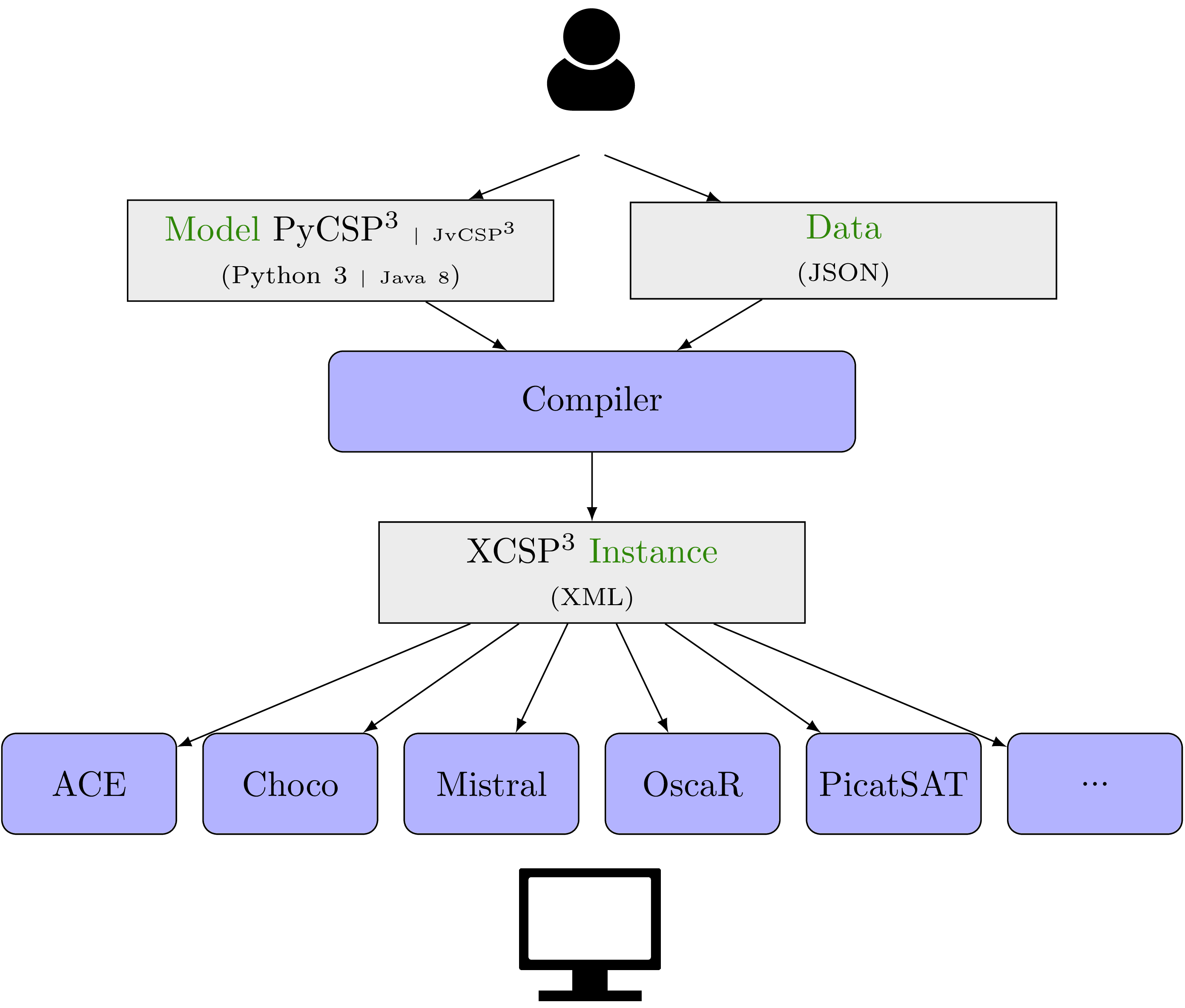
This approach has many advantages:
- Python, JSON, and XML are robust mainstream technologies
- using JSON for data permits to have a unified notation, easy to read for both humans and computers
- using Python 3 for modeling allows the user to avoid learning again a new programming language
- using a coarse-grained XML structure permits to have compact and readable problem instances
Note that using JSON instead of XML for representing instances would have been possible but has some drawbacks, as explained in an appendix of XCSP3 Specifications.


