Constraint MDD

The constraint MDD ensures that the (sequence of) values assigned to the variables of a specified list follows a path going from the root of a specified MDD (Multi-valued Decision Diagram) to its (unique) terminal node.

Because the graph is directed, acyclic, with only one root node and only one terminal node, we just need to introduce the set of transitions.

Interestingly, in PyCSP$^3$, we can directly write constraints MDD in mathematical form, by using tuples, MDDs and the operator ‘in’. The scope of a constraint is given by a tuple of variables on the left of the constraining expression and an MDD is given on the right of the constraining expression. MDDs are objects of the class MDD that are built by specifying a named parameter for the set of transitions, which is technically a set (or list) of 3-tuples.

To see how this constraint works, we need first to import the library PyCSP$^3$:

from pycsp3 import *

For our illustration, we introduce three stand-alone variables $u$, $v$ and $w$, each one with ${0,1,2}$ as domain.

u = Var(0,1,2)
v = Var(0,1,2)
w = Var(0,1,2)

Our objective is to impose that the sequence of values assigned to the variables $u$, $v$ and $w$ belongs to the follwing MDD:

The MDD $M$: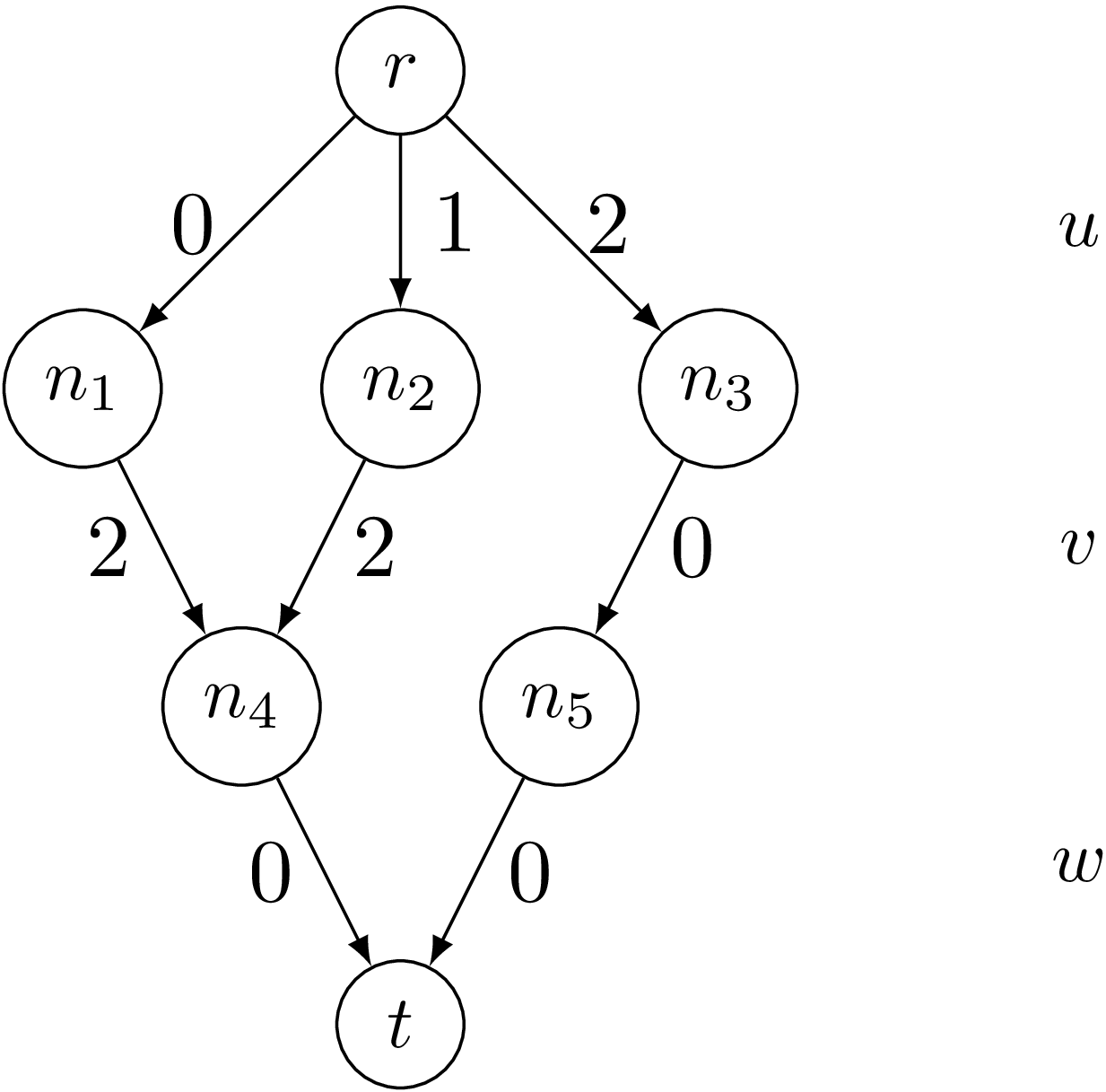

We can represent this MDD $M$ as follows:

r, n1, n2, n3, n4, n5, t = "r", "n1", "n2", "n3", "n4", "n5", "t"  # names of nodes
transitions = [(r,0,n1), (r,1,n2), (r,2,n3), (n1,2,n4), (n2,2,n4), (n3,0,n5), (n4,0,t), (n5,0,t)]
M = MDD(transitions)

We can print the textual representation of the automaton:

print(M)

MDD(transitions={(r,0,n1),(r,1,n2),(r,2,n3),(n1,2,n4),(n2,2,n4),(n3,0,n5),(n4,0,t),(n5,0,t)})

We simply post a single constraint MDD:

satisfy(
    (u,v,w) in M
);

Interestingly, we can also display the internal representation of the posted constraint; although a little bit technical, we can see that the information is correctly recorded.

print(posted())

mdd(list:[u, v, w], transitions:(r,0,n1)(r,1,n2)(r,2,n3)(n1,2,n4)(n2,2,n4)(n3,0,n5)(n4,0,t)(n5,0,t))

By calling the function solve(), we can check that the problem (actually, the single constraint) is satisfiable (SAT). We can also print the values assigned to the variables in the found solution; we can call the function values() that collects the values assigned (in the last found solution) to a specified list of variables.

if solve() is SAT:
    print("Solution: ", value(u), value(v), value(w))

Solution:  0 2 0

On can enumerate the solutions (supports) for this constraint as follows:

if solve(sols=ALL) is SAT:
    for i in range(n_solutions()):
        print(f"Solution {i+1}: {value(u, sol=i)} {value(v, sol=i)} {value(w, sol=i)}")

Solution 1: 0 2 0
Solution 2: 1 2 0
Solution 3: 2 0 0

It is not very surprising to get what was already visible on the MDD.

Related Models