Constraint Cumulative
The constraint Cumulative is useful when a resource of limited quantity must be shared for achieving several tasks. For example, in a scheduling context where several tasks require some specific quantities of a single resource, the cumulative constraint imposes that a strict limit on the total consumption of the resource is never exceeded at each point of a time line. The tasks may overlap but their cumulative resource consumption must never exceed the limit.
In the following figure, five tasks (some of them overlapping) are scheduled while never exceeding the capacity (5) of the resource. The interested reader can check that there is no better scheduling scenario, that is to say, a way of scheduling the five tasks in less than 7 time units. 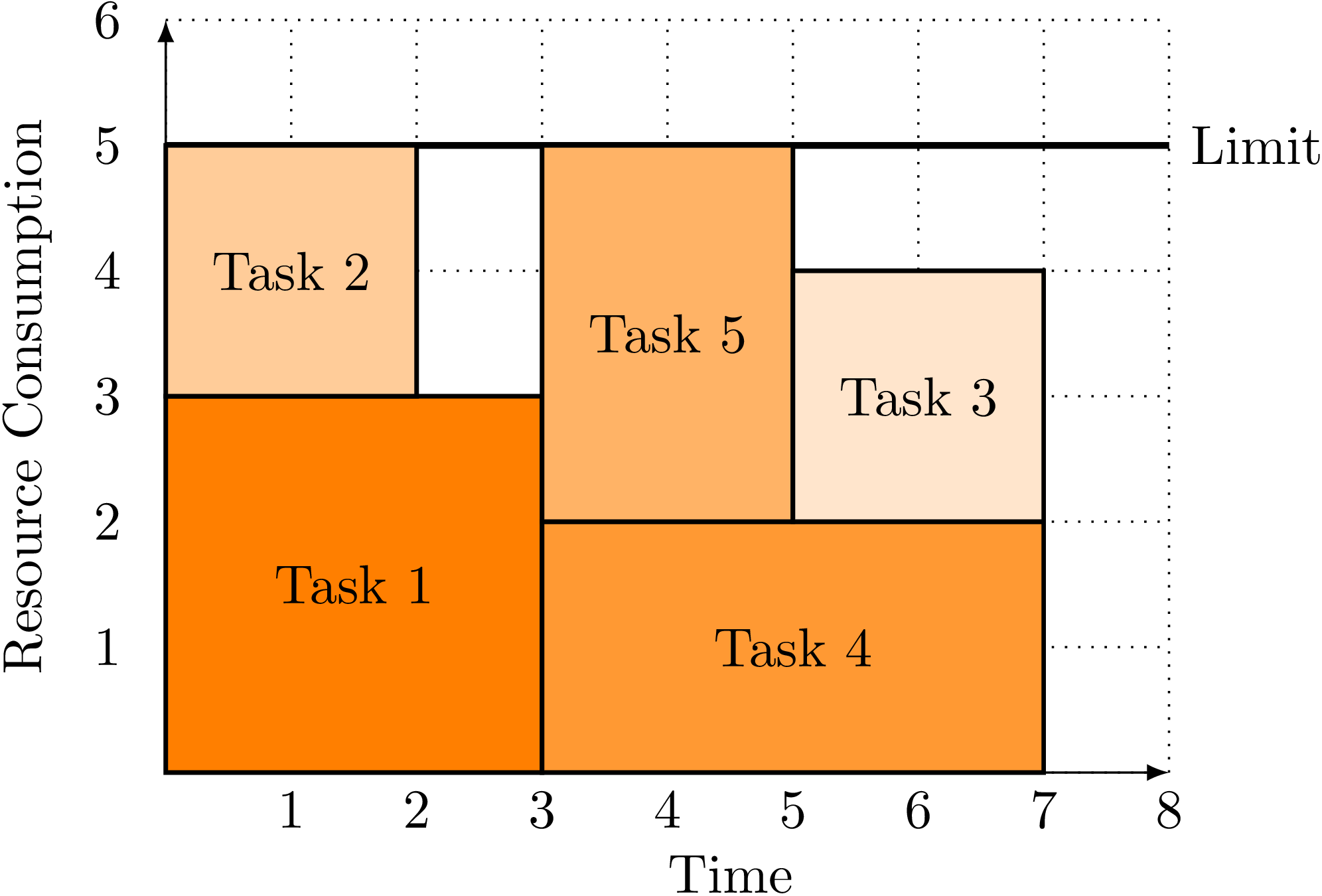
Below, we give some illustrations of the constraint Cumulative.
To see how this constraint works, we need first to import the library PyCSP$^3$:
from pycsp3 import *
For our illustration, we introduce an array $x$ of 5 variables, each one with 0..7 as domain. These variables will correspond to the starting times of 5 tasks.
# x[i] is the starting time of the ith task
x = VarArray(size=5, dom=range(8))
We can display (the structure of) the array as well as the domains of the variables.
print("Array of variable x: ", x)
print("Domain of any variable: ", x[0].dom)
Array of variable x: [x[0], x[1], x[2], x[3], x[4]]
Domain of any variable: 0..7
A first way of posting a constraint Cumulative is to call the function Cumulative() with three named parameters origins, lengths and heights (and possibly, ends). For our illustration, this gives:
satisfy(
Cumulative(origins=x, lengths=[3,2,2,4,2], heights=[3,2,2,2,3]) <= 5
);
We can display the internal representation of the posted constraint; this way, although a little bit technical, we can see that the arguments to the constraint are correct (note that ‘le’ stands for (less than or equal to’).
print(posted())
cumulative(origins:[x[0], x[1], x[2], x[3], x[4]], lengths:[3, 2, 2, 4, 2], heights:[3, 2, 2, 2, 3], condition:(le,5))
By calling the function solve(), we can check that the problem (actually, the single constraint) is satisfiable (SAT). We can also print the values assigned to the variables in the found solution; we can call the function values().
if solve() is SAT:
print("Solution: ", values(x))
Solution: [0, 0, 2, 3, 4]
We can count the number of solutions (supports) to this constraint.
if solve(sols=ALL) is SAT:
print("Number of solutions: ", n_solutions())
Number of solutions: 5760
Using the named Parameter tasks
Instead of using the named parameters origins, lengths and heights (and possibly, ends), one can use a unique named parameter called tasks. Its value must be a list of 3-tuple or 4-tuple, indicating for each task, the origin, the length, and the height of the task.
To illustrate it, we need first to discard the last posted constraint.
unpost()
We can check that there are no more constraints:
print(posted())
[]
We post the same constraint as above, by using tasks:
lengths = [3,2,2,4,2]
heights = [3,2,2,2,3]
satisfy(
Cumulative(tasks=[(x[i],lengths[i],heights[i]) for i in range(5)]) <= 5
);
We can observe that the very same constraint has been posted.
print(posted())
cumulative(origins:[x[0], x[1], x[2], x[3], x[4]], lengths:[3, 2, 2, 4, 2], heights:[3, 2, 2, 2, 3], condition:(le,5))
Another possibility is to use the predefined named tuple Task, as follows:
unpost()
satisfy(
Cumulative(Task(origin=x[i],length=lengths[i],height=heights[i]) for i in range(5)) <= 5
)
print(posted())
cumulative(origins:[x[0], x[1], x[2], x[3], x[4]], lengths:[3, 2, 2, 4, 2], heights:[3, 2, 2, 2, 3], condition:(le,5))
or even to combine the two syntactic sugar mechanisms, as follows:
unpost()
satisfy(
Cumulative(tasks=[Task(origin=x[i],length=lengths[i],height=heights[i]) for i in range(5)]) <= 5
)
print(posted())
cumulative(origins:[x[0], x[1], x[2], x[3], x[4]], lengths:[3, 2, 2, 4, 2], heights:[3, 2, 2, 2, 3], condition:(le,5))