Problem Subgraph Isomorphism

An instance of the subgraph isomorphism problem is defined by a pattern graph $G_p=(V_p,E_p)$ and a target graph $G_t=(V_t,E_t)$: the objective is to determine whether $G_p$ is isomorphic to some subgraph(s) in $G_t$. Finding a solution to such a problem instance means then finding a subisomorphism function, that is an injective mapping $f : V_p \rightarrow V_t$ such that all edges of $G_p$ are preserved: $\forall (v,v’) \in E_p, (f(v_p),f(v’_p)) \in E_t$. Here, we refer to the partial, and not the induced subgraph isomorphism problem.

An Instance of the Subgraph Isomorphism Problem.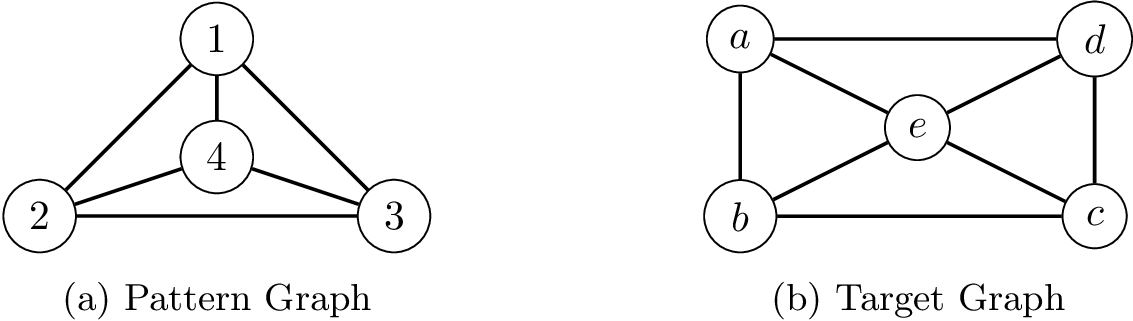

To build a CSP (Constraint Satisfaction Problem) model, we need first to import the library PyCSP$^3$:

from pycsp3 import *

Then, we need some data. For example, for the two graphs shown above, we can write:

n = 4  # number of nodes in the pattern graph
m = 5  # number of nodes in the target graph
p_edges = [(0,1), (0,2), (0,3), (1,2), (1,3), (2,3)]
t_edges = [(0,1), (0,3), (0,4), (1,2), (1,4), (2,3), (2,4), (3,4)]

In the pattern graph, we have 4 nodes and 6 edges, whereas in the target graph, we have 5 nodes and 8 edges. Note that we use indexes for nodes (for example, index 0 is used for node 1 in the pattern graph and for node a in the target graph).

We start our CSP model by introducing an array $x$ of variables.

# x[i] is the target node to which the ith pattern node is mapped
x = VarArray(size=n, dom=range(m))

We can display the structure of the array, as well as the domain of the first variable (note that all variables have the same domain).

print("Array x: ", x)
print("Domain of any variable in x: ", x[0].dom)

Array x:  [x[0], x[1], x[2], x[3]]
Domain of any variable in x:  0..4

Concerning the constraints, we have to post first a constraint AllDifferent.

satisfy(
   # ensuring injectivity
   AllDifferent(x)
);

Interestingly, by calling the function solve(), we can check that the problem is satisfiable (SAT). We can also display the found solution. Here, we call the function values() that collects the values assigned to a specified list of variables.

if solve() is SAT:
    print(values(x))

[0, 1, 2, 3]

It works, but edges are not preserved. We need a table for enumerating all possible mappings of any pattern edge:

T = {(i, j) for (i, j) in t_edges} | {(j, i) for (i, j) in t_edges}

We can now post a group of constraints Extension.

satisfy(
    # preserving edges
    (x[i], x[j]) in T for (i, j) in p_edges
);

We can display the internal representation of the posted constraints; this way, although a little bit technical, we can see that everything we need is present.

print(posted())

allDifferent(list:x[])
extension(list:[x[0], x[1]], supports:(0,1)(0,3)(0,4)(1,0)(1,2)(1,4)(2,1)(2,3)(2,4)(3,0)(3,2)(3,4)(4,0)(4,1)(4,2)(4,3))
extension(list:[x[0], x[2]], supports:(0,1)(0,3)(0,4)(1,0)(1,2)(1,4)(2,1)(2,3)(2,4)(3,0)(3,2)(3,4)(4,0)(4,1)(4,2)(4,3))
extension(list:[x[0], x[3]], supports:(0,1)(0,3)(0,4)(1,0)(1,2)(1,4)(2,1)(2,3)(2,4)(3,0)(3,2)(3,4)(4,0)(4,1)(4,2)(4,3))
extension(list:[x[1], x[2]], supports:(0,1)(0,3)(0,4)(1,0)(1,2)(1,4)(2,1)(2,3)(2,4)(3,0)(3,2)(3,4)(4,0)(4,1)(4,2)(4,3))
extension(list:[x[1], x[3]], supports:(0,1)(0,3)(0,4)(1,0)(1,2)(1,4)(2,1)(2,3)(2,4)(3,0)(3,2)(3,4)(4,0)(4,1)(4,2)(4,3))
extension(list:[x[2], x[3]], supports:(0,1)(0,3)(0,4)(1,0)(1,2)(1,4)(2,1)(2,3)(2,4)(3,0)(3,2)(3,4)(4,0)(4,1)(4,2)(4,3))

We can run again the solver.

if solve() is SAT:
    print(values(x))

Nothing is displayed. This is because the result is UNSAT, which is confirmed by executing:

status = solve()
print("Status: ", status)

Status:  UNSAT

The instance is unsatisfiable because there is no 4-clique (4 nodes that are all linked each other) in the target graph.

We propose to modify the target graph by adding an edge between the nodes a and c, before updating the constraints Extension. First, we modify the table:

T = T | {(0,2), (2,0)}

We check it:

print(T)

{(0, 1), (2, 4), (1, 2), (0, 4), (3, 4), (4, 0), (2, 1), (4, 3), (0, 2), (1, 0), (3, 2), (4, 1), (0, 3), (2, 0), (1, 4), (4, 2), (2, 3), (3, 0)}

The we remove all constraints that were posted during the last call to satsify(). This is possible by executing:

unpost()

We control that there is only the constraint AllDifferent left.

print(posted())

allDifferent(list:x[])

Finally, we post the new table constraints:

satisfy(
    # preserving edges
    (x[i], x[j]) in T for (i, j) in p_edges
);

And we run the solver:

if solve() is SAT:
    print(values(x))

[0, 1, 2, 4]

We can check that 48 solutions exist, as follows.

if solve(sols=ALL) is SAT:
    print("Number of solutions: ", n_solutions())

Number of solutions:  48

Finally, we give below the model in one piece. Here the data is expected to be given by the user (in a command line). We also pay attention to possible self loops.

from pycsp3 import *

n, m, p_edges, t_edges = data

p_loops = [i for (i, j) in p_edges if i == j]
t_loops = [i for (i, j) in t_edges if i == j]
T = {(i, j) for (i, j) in t_edges} | {(j, i) for (i, j) in t_edges}


# x[i] is the target node to which the ith pattern node is mapped
x = VarArray(size=n, dom=range(m))

satisfy(
    # ensuring injectivity
    AllDifferent(x),

    # preserving edges
    [(x[i], x[j]) in T for (i, j) in p_edges],

    # being careful of self-loops
    [x[i] in t_loops for i in p_loops]
)