CSP easy

Problem Rectangle Packing

The rectangle packing problem consists of finding a way of putting a given set of boxes (rectangles) in a container (enclosing rectangle) without overlap.

Here is an example of packing 11 rectangles (boxes) in a container: 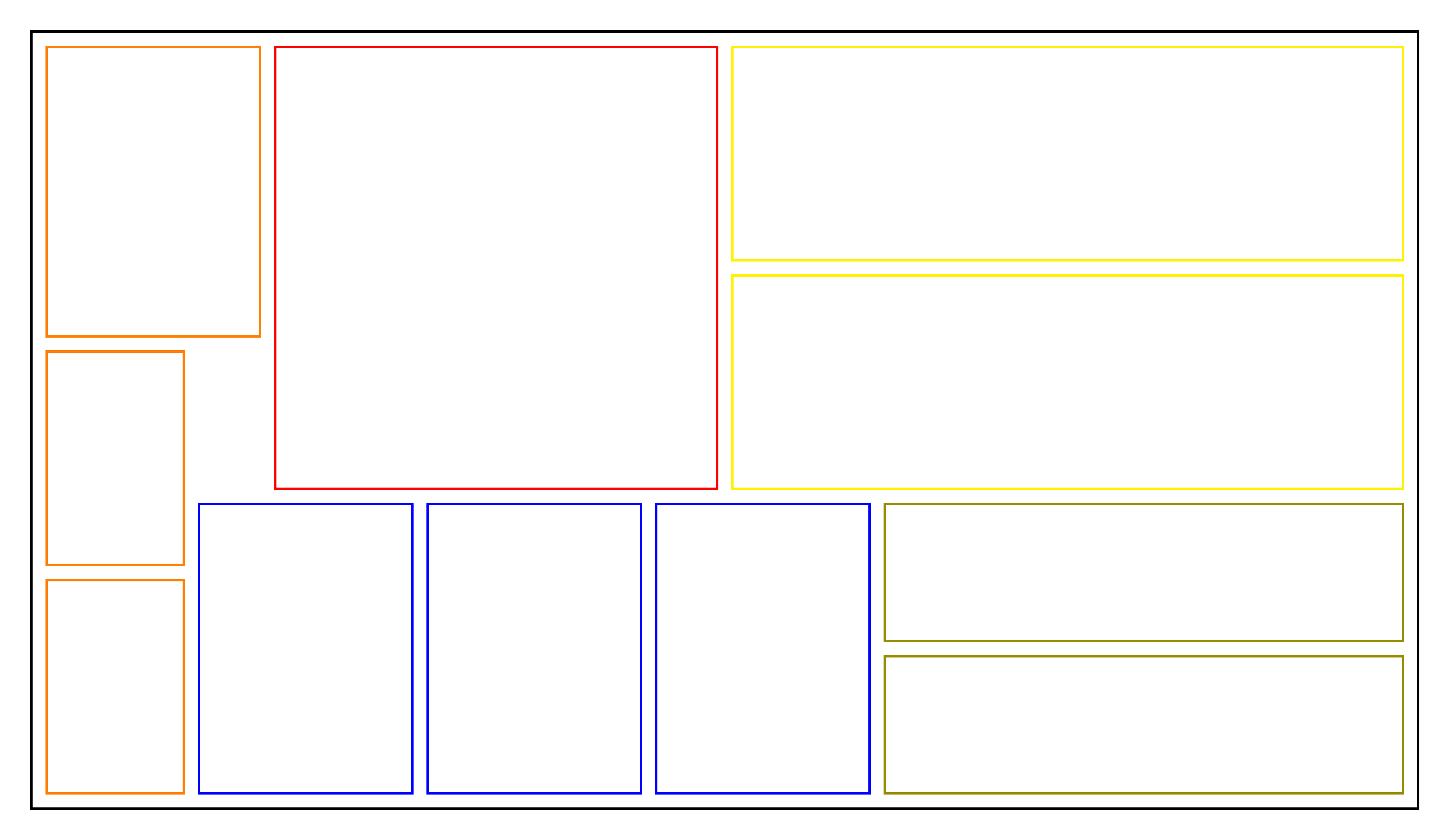rectangle packing

To build a CSP (Constraint Satisfaction Problem) model, we need first to import the library PyCSP$^3$:

from pycsp3 import *

Then, we need some data. Here, we define the width and height of the container, as well as the list of boxes to be packed in the container (we use named tuples to represent them).

Box = namedtuple('Box', 'width height')

width, height = 8, 7   # size of the container}
boxes = [Box(2, 2), Box(4,2), Box(3,3), Box(5,4), Box(4,3)]
nBoxes= len(boxes)

We start our CSP model with two arrays $x$ and $y$ of variables; we have two variables per box, one for its position along the x-axis and the other for its position along the y-axis (with respect to the container).

# x[i] is the x-coordinate where is put the ith box
x = VarArray(size=nBoxes, dom=range(width))

# y[i] is the y-coordinate where is put the ith box
y = VarArray(size=nBoxes, dom=range(height))

To control that everything is fine, we can display the structures of the two arrays as well as, for example, the domain of the variables associated with the first box (with index 0).

print("Array of variables x: ", x)
print("Array of variables y: ", y)
print("Domain of x[0]: ", x[0].dom)
print("Domain of y[0]: ", y[0].dom)

Array of variables x:  [x[0], x[1], x[2], x[3], x[4]]
Array of variables y:  [y[0], y[1], y[2], y[3], y[4]]
Domain of x[0]:  0..7
Domain of y[0]:  0..6

Concerning the constraints, to start, we need to guarantee that the boxes remain within the perimeter of the container. For this purpose, we introduce two lists of unary constraints:

satisfy(
    # unary constraints on x
    [x[i] + boxes[i].width <= width for i in range(nBoxes)],

    # unary constraints on y
    [y[i] + boxes[i].height <= height for i in range(nBoxes)]
);

We can print the intern representation of the constraints that have been posted. Athough a little bit technical, one can see that we have two constraints Intension per box (note that ‘le’ stands for ‘less than or equal to’).

print(posted())

intension(function:le(add(x[0],2),8))
intension(function:le(add(x[1],4),8))
intension(function:le(add(x[2],3),8))
intension(function:le(add(x[3],5),8))
intension(function:le(add(x[4],4),8))
intension(function:le(add(y[0],2),7))
intension(function:le(add(y[1],2),7))
intension(function:le(add(y[2],3),7))
intension(function:le(add(y[3],4),7))
intension(function:le(add(y[4],3),7))

We can now post the 2-dimensional form of the constraint NoOverlap (which is also sometimes called diffn in the litterature). It ensures that, given a set of 2-dimensional boxes; for any pair of such boxes, there exists at least one dimension where one box is after the other, i.e., the boxes do not overlap.

satisfy(
    # no overlap on boxes
    NoOverlap(origins=[(x[i],y[i]) for i in range(nBoxes)], lengths=boxes)
);

Interestingly, by calling the function solve(), we can check that the problem is satisfiable (SAT). We can also display the position of the boxes in the solution that has been found.

if solve() is SAT:
    for i in range(nBoxes):
        print(f"The box {i} is at ({value(x[i])},{value(y[i])})")

The box 0 is at (0,0)
The box 1 is at (0,5)
The box 2 is at (0,2)
The box 3 is at (3,0)
The box 4 is at (4,4)

On this simple problem instance, we can easily count the number of distinct solutions (but note that some of them may be symmetric).

if solve(sols=ALL) is SAT:
    print("Number of solutions: ", n_solutions())

Number of solutions:  16

We can also display all solutions as follows.

if solve(sols=ALL) is SAT:
    for i in range(n_solutions()):
        print(f"Solution {i+1}: {values(x, sol=i)} {values(y, sol=i)}")

Solution 1: [0, 0, 0, 3, 4] [0, 5, 2, 0, 4]
Solution 2: [0, 0, 0, 3, 4] [3, 5, 0, 0, 4]
Solution 3: [0, 0, 0, 3, 4] [5, 0, 2, 3, 0]
Solution 4: [0, 0, 0, 3, 4] [2, 0, 4, 3, 0]
Solution 5: [1, 0, 0, 3, 4] [2, 0, 4, 3, 0]
Solution 6: [5, 4, 5, 0, 0] [2, 0, 4, 3, 0]
Solution 7: [6, 4, 5, 0, 0] [2, 0, 4, 3, 0]
Solution 8: [6, 4, 5, 0, 0] [3, 5, 0, 0, 4]
Solution 9: [5, 4, 5, 0, 0] [3, 5, 0, 0, 4]
Solution 10: [5, 4, 5, 0, 0] [0, 5, 2, 0, 4]
Solution 11: [6, 4, 5, 0, 0] [0, 5, 2, 0, 4]
Solution 12: [1, 0, 0, 3, 4] [0, 5, 2, 0, 4]
Solution 13: [1, 0, 0, 3, 4] [5, 0, 2, 3, 0]
Solution 14: [5, 4, 5, 0, 0] [5, 0, 2, 3, 0]
Solution 15: [6, 4, 5, 0, 0] [5, 0, 2, 3, 0]
Solution 16: [1, 0, 0, 3, 4] [3, 5, 0, 0, 4]

Finally, we give below the model in one piece. Here the data is expected to be given by the user (in a command line).Note that when the container is a square, we can post some symmetry-breaking constraints.

from pycsp3 import *

width, height = data.container
boxes = data.boxes
nBoxes = len(boxes)

# x[i] is the x-coordinate where is put the ith box (rectangle)
x = VarArray(size=nBoxes, dom=range(width))

# y[i] is the y-coordinate where is put the ith box (rectangle)
y = VarArray(size=nBoxes, dom=range(height))

satisfy(
    # unary constraints on x
    [x[i] + boxes[i].width <= width for i in range(nBoxes)],

    # unary constraints on y
    [y[i] + boxes[i].height <= height for i in range(nBoxes)],

    # no overlap on boxes
    NoOverlap(origins=[(x[i], y[i]) for i in range(nBoxes)], lengths=boxes),

    # tag(symmetry-breaking)
    [
      x[-1] <= math.floor((width - boxes[-1].width) // 2.0),
      y[-1] <= x[-1]
    ] if width == height else None
)