Quick Start

In this page, we give a quick illustration about how to build a simple model.

The first thing to do is to import the library PyCSP$^3$:

from pycsp3 import *

If you have a problem, this is certainly because you need the Python package pycsp3 to be installed on your system. You need to execute something like pip install pycsp3. See the Installation Page.

For our illustration, the problem is to color the nodes of a complete graph (later, we introduce the conditions to be respected). We consider here a complete graph with 4 nodes: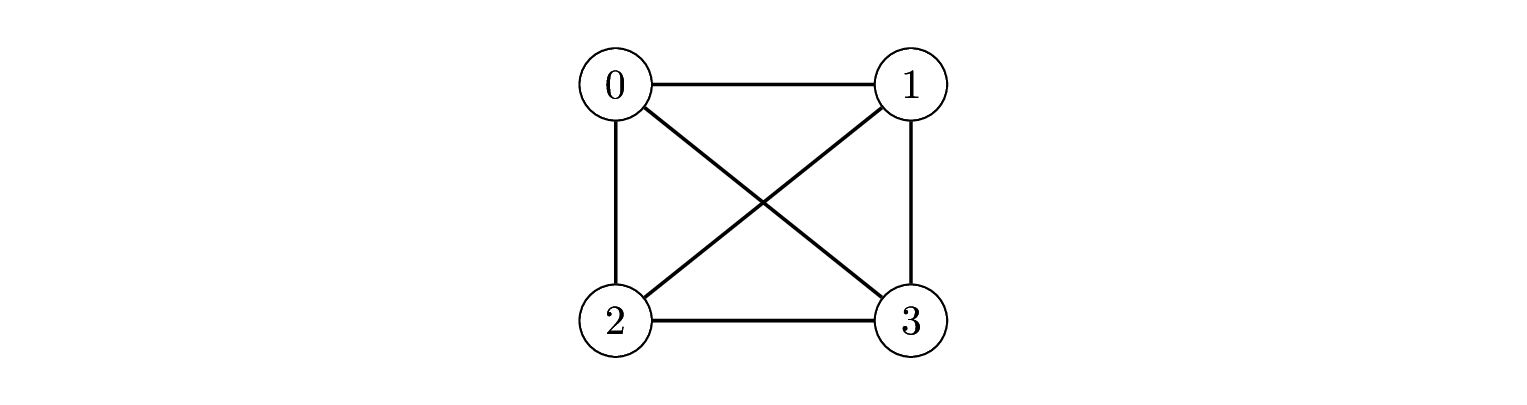

We use a constant n to denote the number of nodes:

n = 4

Finding a color to each node implies that we introduce a variable with each node. Let us suppose that we have 3 colors only. We can then write:

R, G, B = colors = 0, 1, 2

# x[i] is the color of the ith node
x = VarArray(size=n, dom=colors)

We can display the structure of the array, as well as the domain of the first variable (note that all variables have the same domain).

print("Array x: ", x)
print("Domain of any variable: ", x[0].dom)

Array x:  [x[0], x[1], x[2], x[3]]
Domain of any variable:  0 1 2

Let us suppose that all nodes with even indexes must have a different color, as well as nodes with odd indexes. We then have two constraints to be satisfied here. We post the two constraints by passing them as parameters of the function satisfy():

satisfy(
    x[0] != x[2],

    x[1] != x[3]
);

Interestingly, by calling the function solve(), we can check that the problem is satisfiable (SAT). We can also display the found solution. Here, we call the function values() that collects the values assigned to a specified list of variables.

if solve() is SAT:
    print(values(x))

[0, 0, 1, 1]

This solution corresponds to: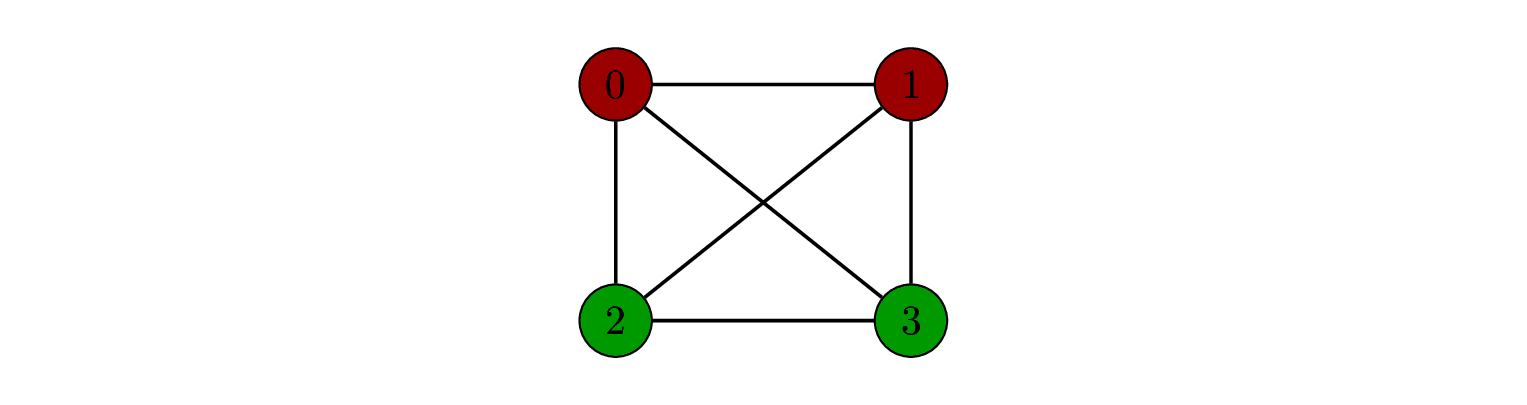

Let us add the following constraints with respect the other edges:

satisfy(
    x[0] != x[1],

    x[1] == x[2],
    
    x[2] != x[3],
    
    x[3] == x[0]
);

We can run the solver again:

if solve() is SAT:
    print(values(x))

[0, 1, 1, 0]

This solution corresponds to: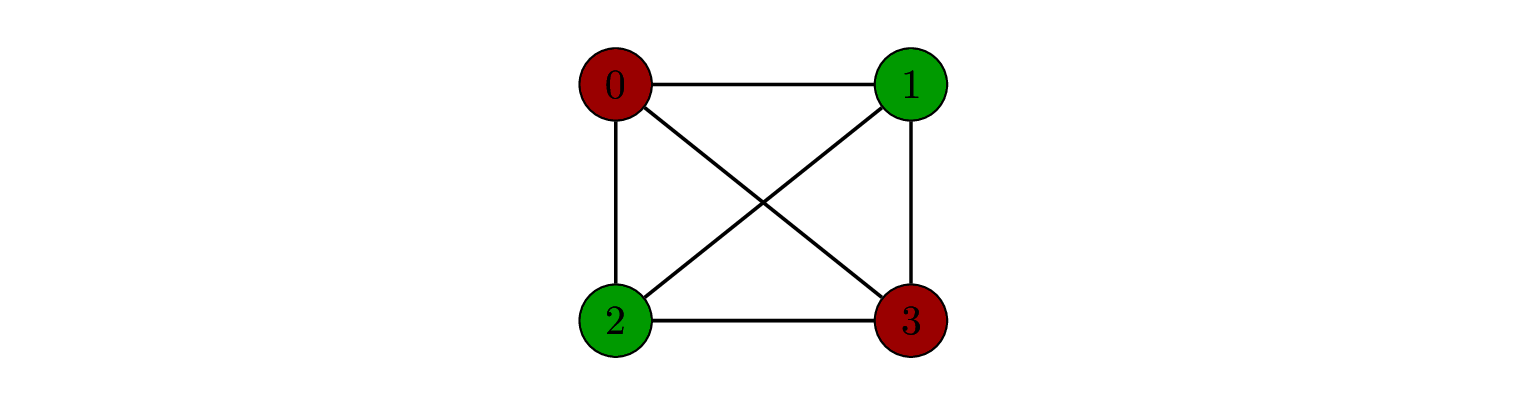

We can check that 6 solutions exist:

if solve(sols=ALL) is SAT:
    print("Number of solutions: ", n_solutions())

Number of solutions:  6