Problem Golomb Ruler
A Golomb ruler is defined as a set of $n$ integers $0 = a_1 < a_2 < … < a_n$ such that the $n \times (n-1)/2$ differences $a_j - a_i$, $1 \leq i < j \leq n$, are distinct. Such a ruler is said to contain $n$ marks (or ticks) and to be of length $a_n$. The objective is to find optimal rulers (i.e., rulers of minimum length).
An optimal Golomb ruler with 4 ticks. 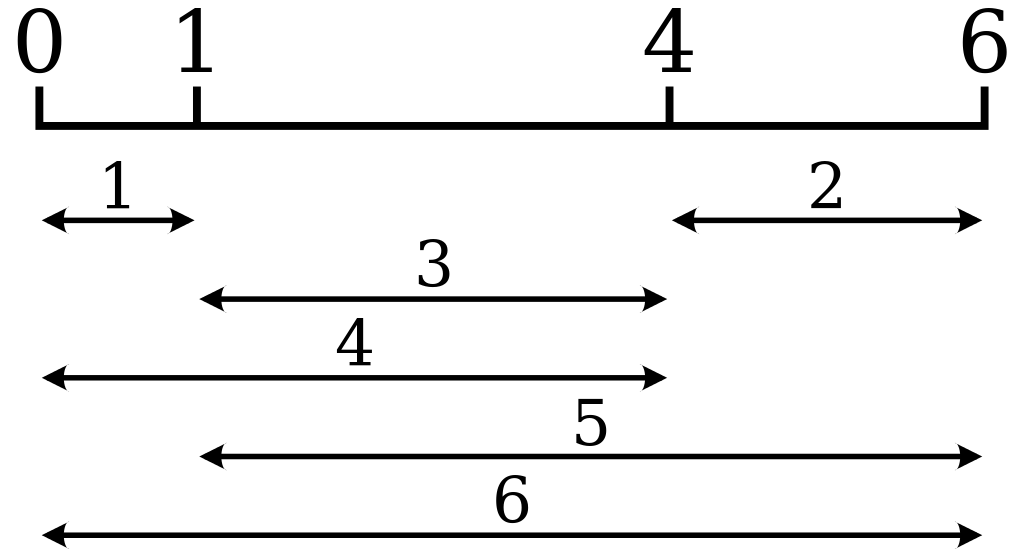
This problem (and its variants) is said to have many practical applications including sensor placements for x-ray crystallography and radio astronomy.
Dimitromanolakis has computed relatively short Golomb rulers and thus showed with computer aid that the optimal ruler for $n \leq 65,000$ has length less than $n^2$.
To build a COP (Constraint Optimization Problem) model, we need first to import the library PyCSP$^3$:
from pycsp3 import *
Then, we need some data. Actually, we just need an integer $n$.
n = 4
We start our COP model by introducing an array $x$ of variables. Becasue Dimitromanolakis has computed relatively short Golomb rulers, and thus showed with computer aid that the optimal ruler for $n \leq 65,000$ has length less than $n^2$, we use $n^2$ as upper bound of the domains of the variables of $x$.
# x[i] is the position of the ith tick
x = VarArray(size=n, dom=range(n * n))
We can display the structure of the array, as well as the domain of the first variable (remember that all variables have the same domain).
print("Array x: ", x)
print("Domain of any variable: ", x[0].dom)
Array x: [x[0], x[1], x[2], x[3]]
Domain of any variable: 0..15
A simple model involves a single constraint AllDifferent that takes as parameters a list of expressions (and not directly some variables of our model).
satisfy(
# all distances are different
AllDifferent(abs(x[i] - x[j]) for i, j in combinations(n, 2))
);
Interestingly, by calling the function solve(), we can check that the problem is satisfiable (SAT. We can also display the found solution. Here, we call the function values() that collects (in the last found solution) the values assigned to a specified list of variables.
if solve() is SAT:
print(values(x))
[1, 0, 3, 7]
The obtained solution does not necessarily give the ticks in increasing order. It means that many symmetries exist. We can break them by setting the first tick at 0, and ensuring a strict order with a constraint Increasing:
satisfy(
# tag(symmetry-breaking)
[x[0] == 0, Increasing(x, strict=True)]
);
Tagging (the list containing) these two constraint is relevant because it clearly informs us that they are inserted for breaking symmetries (and besides, tags may be exploited by solvers). Tagging is made possible by putting in a comment line an expression of the form tag(), with a token (or a sequence of tokens separated by a white-space) between parentheses.
We can run again the solver.
if solve() is SAT:
print(values(x))
[0, 1, 3, 7]
This time, all ticks are increasingly given.
Concerning optimization, we want to minimize the length of the rule, which is equivalent to minimize the value of the rightmost variable (tick).
minimize(
# minimizing the position of the rightmost tick
x[-1]
);
We can run again the solver, with this optimization task. Note that we need to check that the status returned by the solver is now OPTIMUM.
if solve() is OPTIMUM:
print(values(x))
[0, 1, 4, 6]
This time, we have an optimal Golomb ruler of length 6 (for 4 ticks).
We invite the reader to change the value of $n$ at the top of this page, and to restart the Jupyter kernel.
Finally, we give below the model in one piece. Here the data is expected to be given by the user (in a command line).
from pycsp3 import *
n = data
# x[i] is the position of the ith tick
x = VarArray(size=n, dom=range(n * n))
satisfy(
# all distances are different
AllDifferent(abs(x[i] - x[j]) for i, j in combinations(n, 2)),
# tag(symmetry-breaking)
[x[0] == 0, Increasing(x, strict=True)]
)
minimize(
# minimizing the position of the rightmost tick
x[-1]
)